ベクトル—複数の値を集めたものRは、複数の値を一つに処理することが容易な言語です。 「複数の数を集める」ことの基本をベクトルといいます(後でこの定義を修正しますが、今はこのように理解してほしい)。ベクトルの作成ベクトルは関数cを利用して作ります。 次は、1、3、5という3つの数を集めてベクトルにして変数xに代入し、3、4、5という3つの数を集めてベクトルにした変数yに代入した例です。

x <-c(1、3、5) #1、3、5で作ったベクターy <-c(3、4、5) #3、4、5で作ったベクター

今の例ではxの要素は最初の項が1、公差が2の等差数列であり、yの要素は最初の項が3、公差が1の等差数列です。 このような要素が等次数列のベクトルをC関数を使わずにより簡単にするために表記法と関数を使用します。課題2-1 次の例を実行してベクトルを作る関数seqの引数の意味を説明せよ

x1 μ-seq(1,5,2) 및 1 μ-seq(3,5) v1 μ-seq(5,1) w1 μ-seq(5,1,-2)

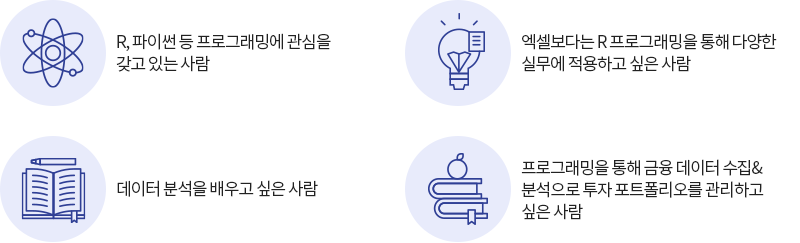
次の例を実行して、ベクトルを作る表記法の数1:数2によってどのようにベクトルが作られるかを説明せよ。

y2 — 3:5 v2 — 5:1
次の例を実行してベクトルを作る関数repの引数の意味を説明せよ
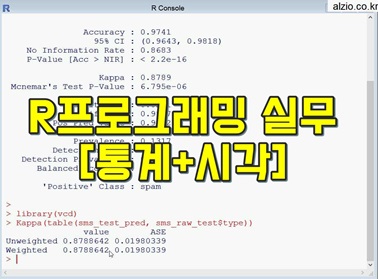
z1 <-rep(1:3,5) z2 <-rep(5:1,3)

ベクトルの演算Rの面白い(初心者の中でなかなか慣れない)部分は、本来は1つの数に対する演算と関数がベクトルでも使えるという点です。まず、四則演算から見てみましょう。 xとyの値を次のように決めてみましょう。

x <-c(1、3、5) #1、3、5からなるベクトルy <-c(3、4、5) #3、4、5からなるベクトル

これを四則演算した結果は以下のとおりです:
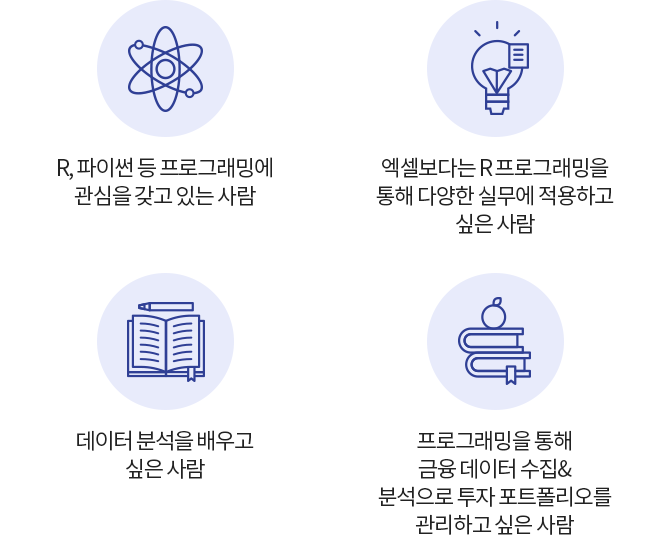
> x + y # c (1,3.5) + c (3,4.5) [1] 4 7 10 # (1+3,3+4,5+5) > x – y # c (1,3,4,4) [1] -2-10 # (1-3,3-4 、5-5) > x * c (1.5)つまり、ベクトル同士の四則演算がベクトル要素間の演算になるのです。次にベクトル1つに対する数を四則演算をしてみましょう。 その結果は以下の通りです。> x + 10 # c(1,3,5) + 10 [1] 11 13 15 # c(1+10, 3+10, 5+10) > x – 10 – 10 – 10 – 7 – 5 [1] – 9 – 7 – 5 – 10 101 0.3 0.5 # c(1/10, 3/10, 5/10)つまり、ベクトルに対してスカラーを四則演算すると、ベクトルの要素それぞれがスカラーと四則演算することになるのです。*訳者注:下表で単一データと表現したものがスカラーらしい。 急に目立つ専門用語にびっくりww同様の方法で関数についても成立します。 sqrtやlogのような関数は1つの数に対して適用されるものです。 しかし、Rではこれもベクトルに適用できます。同様の方法で関数についても成立します。 sqrtやlogのような関数は1つの数に対して適用されるものです。 しかし、Rではこれもベクトルに適用できます。logやsqrtが本来は1つの数を引数として持つのに対し、平均値と最大値、最小値を求める関数はベクトルのような複数の値に対して積まれる関数です。 そしてRでは、そのようなベクトルを引数とする関数がたくさんあります。 それをいくつかご紹介します。length #ベクトルの要素個数を求める max #最大値を求める min #最小値を求める mean #平均値を求める range #値の範囲を求める rev #要素を逆順にする sd #要素偏差を求める sort #要素を整列(sort)する sum#要素の和が求める var#分散が求められる課題2-2x <-c(1、6、8、-4、2) #1、6、8、-4、2人ベクトルであるとき、ベクトルの演算に挙げた例を実行して、値を求めなさい。 その結果によって関数の意味を確認してみよう。ベクトルの要素ベクトルの中のそれぞれの数値を「要素」と呼びます。 ベクトルの特定の要素だけを取り出して、あるいは特定の要素を抜いたベクトルを求めるときの方法などについて話してみます。 プログラミング言語Cとは異なり、ベクトルの要素番号は0ではなく1から始まります。ベクトルの特定の要素を参照する(値を取り出す)ときは、要素の番号を各括弧([ ])内に指定します。 そして、要素の番号でベクトルを指定すると、複数の要素をベクトルから取り出すこともできます。 さらに、下記の例の最後の行のように[ ]の中に条件式を書けば、その条件に満足する要素のみを持つベクトルを返すことができます。> x <-c(1、3、5、-4、2) #1、3、5、-4、2を持つベクトル> x[1] #1番目にある要素の値[1] 1 > x[length(x)] #length(x)=5なのでxの最後に入っている値を表す[1] 2 > x [100] # 100番目を呼び出しても要素はない [1] NA > x [2:4] #2番目から4番目までの要素 [1] 35 – 4 > x [c(5, 3, 3, 3, 3, 3, 3, 3··· [1] 3-4 # その番地に入っていた要素だけを除いたベクトルを返還> x[x < 3] # x< 3という条件を満たす要素を取り出そうとする[1] 1-42課題2-3z<-c(30、33、29、38、49、9、42、29、7、7、41、24、46、39、7、27、30、16、40、37、2)の場合(1)zの要素の中に30以下のものから整列するベクトルを返す式(2)zの要素で30より大きい要素の平均値を求める式(3)zの要素を小さいものから整列する際に、一番前から5番目まで要素を返す式(4)zの要素で奇数のみベクトルに返す式を、セラベクターの特定要素を別要素に変えることも可能である。 そのためには、ベクトルの特定の要素を取り出す式を書き、それに他の要素を「代入」する、という式を書けばよい。(以下では;を書いているが、それは複数の命令文を一行で書くための表記法である)> x <-c(1、3、5、-4、2) #1、3、5、-4、2が含まれたベクトル> x[1] <-10; x #x[1]に10を代入 [1] 10 6 8 -4 2 # x[1]が10に変わる > x[10] <-10 ; x # 10番目の要素は存在しないが··· [1] 10 3 5 – 4 2 NA NA 10 #x[10]に10を代入し、存在しない要素はNAが入る>x[6:9]< – 0; x # 6番目から9番目までの要素に0を代入 [1] 10 3 5 – 4 2 0 0 0 0 0 # 6番目から9番目までの要素が0になる> x[c(3, 1, 5)] < – c(20, 30, 40) ; x # 3, 1, 5番目の要素に 20, 40を代入 [1] 30 – 4 0, 3 20 – 4 0.5 # 320、 40になる> x[x < 3] <-50; x # x< 3という条件を満たす要素に50を代入する[1] 30 3 20 50 40 50 50 10 # x< 3という条件を満たす要素が50になる> x <-c(1、3、5、-4、2) #1、3、5、-4、2が含まれたベクトル> x[1] <-10; x #x[1]に10を代入 [1] 10 6 8 -4 2 # x[1]が10に変わる > x[10] <-10 ; x # 10番目の要素は存在しないが··· [1] 10 3 5 – 4 2 NA NA 10 #x[10]に10を代入し、存在しない要素はNAが入る>x[6:9]< – 0; x # 6番目から9番目までの要素に0を代入 [1] 10 3 5 – 4 2 0 0 0 0 0 # 6番目から9番目までの要素が0になる> x[c(3, 1, 5)] < – c(20, 30, 40) ; x # 3, 1, 5番目の要素に 20, 40を代入 [1] 30 – 4 0, 3 20 – 4 0.5 # 320、 40になる> x[x < 3] <-50; x # x< 3という条件を満たす要素に50を代入する[1] 30 3 20 50 40 50 50 10 # x< 3という条件を満たす要素が50になる関数の作り方ここでは、関数の定義を中心に説明します。関数というのは、与えられた入力に基づいて何かを計算して出力を返すことです。 R では、この定義に従って関数定義の基本形を次のように定めています。関数名 <-function(カイン数1、カイン数2、…) {関数本体}見ればわかりますが、「関数名」の値で関数の定義を設定します。 「カイン数」とは入力を記憶するための変数を意味し、「関数本体」で計算されます。 関数本体中にreturn文が実行されると、計算が終わり、returnの引数が関数全体の結果として出力されます。 そうでなければ、関数本体の最後の文章の値が返されます。以下は関数定義の例ですが、ベクトルを入力としてその要素の二乗の和を返します。スクエア.sum^- 関数(x)^ 及びsum(x*x) return(y)^[上記の関数の追加説明] この例は、変数yを使わなくても次のように書くことができる。square.sum1 <-function(x) {return(sum(x*x))}そうすれば、関数本体は一文だけ書けばいいので、returnを使わなくてもいいです:square.sum2 <- 関数(x)sum(x*x)ここで{}までなくさなければならないことに注意してください。 これが正しく元の関数square.sumと同じ結果を返すことを確認してほしい、ここでxやyは関数square.sumに使われる「地域変数」であり、その中でのみ値が有効です。 また、例えば次のように関数の外で使われるとしても、関数とは関係なく使われることに留意しましょう。> x <-3; y <-5 #;を書けば複数の命令文を一行に書くことができる> square。sum(1,2,3) # square。sum+呼ぶ [1] 14 # square。sum+y <> 印刷(y) # 元 y 値 [1] 5題2-4 제곱sumの定義を参照して、ベクトルを入力して「その平均値と各要素の差」の二乗を返す関数ex2.4を書いてみよう。 言い換えれば、入力ベクトルをc(x1、x2、…、xn)に置き、その平均値をmとすると、(x1-m)^2 + (x2-m)^2 +··· + (xn-m)^2 を返す関数を作れということだ。参考R の中で関数と変数値を「編集」(修正と追加、一部削除すること)できます。(ただし、ある値が入った変数でなければなりません)例えば、関数ex 2.4 の定義を編集するには、ex2.4 < – 編集(ex2.4)と言えばいいのです。 別のウィンドウが開き、ex2.4の値、つまり関数を編集することができます。このページのR関数と記号산술연산자: + - * / %/% %% ^ **비교연산자: == != >= > <= <논리연산자: ! & |: #: # 수수:an2cost infhrt10정석 & pi切りの井 a天ア捨 sq # | in&anh hasat sin expロサ cos logフド| null NUX( とbreak min mean var 数 の ) 照 参 : 「 ( を 게 에 ピ null 에 na ナ 게 로編集산술연산자: + - * / %/% %% ^ **비교연산자: == != >= > <= <논리연산자: ! && ||석학: #수수 함수: sincostan sinh cosh tan has in a cosatan log2 log10 exp sqrt ラウンドフロア天井の切り捨てサインabs정: pi Inf NULL NA TRUE FALSE FALSE(変名としдえ):break else 関数の FALSE(Inf の場合) ナナネクス NULL リピート TRUE while: c : seq rep 터에게 보내는 답로 : length max min mean range revs sort sum var함에게 보내는 답를: function, return, return, return、「(」を参照)」:編集[課題2-1の答え]実行してみるとわかるように、seq(n1, n2, n3)は最初の項が n1、最後の項が n2、公差が n3(省略した場合は 1、ただし n1 > n2 の場合は -1)の等差数列の要素からなるベクトルを返します。> x1 <-seq (1.5.2 ) > y1 <-seq (3.5 ) > v1 <-seq (5.1 ) > w1 <-seq (5.1 、-2 ) > x1 [1] 1 3 5 > y1 [1] 3 4 5 > v1 [1] 5 4 2 1実行してみればわかるように、n1:n2は、最初の項がn1、最後の項がn2、公差が1(ただしn1 > n2 の場合は-1)の等差数列を要素とするベクトルを返します。> (y2 <-3:5> [1] 3 4 5 > (v2 <-5:1) [1] 5 4 3 21実行すればわかるように、rep(n1、n2)はn1をn2回繰り返すベクトルを返します。> (z1 <-rep(1:3.5)) [1] 1 2 3 1 2 2 1 2 2 2 > (z2 <-rep(5:1.3)) [1] 5 4 3 1 5 3 4 3 5 3 1 5 4 3 21[課題2-2の答え]x <-c(1、6、8、-4、2) #1、6、8、-4、2を持つベクトル> length(x) #ベクトルの要素数を求める [1] 5 #xは5つの要素を持っている > max(x) #最大値を求める [1] 8 #最大値は 8 > min(x) #最小値を求める [1] -4 #最小値は -mean(x) #平均値を求める [1] 2.6#sum(x)/length(x)/length(ge)とも同じ範囲> 4.669047 #sqrt(var(x))と同じ > sort(x) #要素を整列(sort)する [1] – 4 1 2 6 8 #要素を昇順(小さいものから大きい数で)立てたベクトル> sum(x) #要素の和を求める [1] 13 # 1 + 6 + 8 – 4 + 2 = 13 > var(x) # 分散を求める [1] 21.8 # 「要素と平均値の差を平方」した合計を、要素数-1で割る[課題2-3の答え]zの要素として30以下のものを持つベクトルを求める:[ ]の中に「z(の要素)が30以下」、という条件を書く>z[z<=30] [1] 30 299 297 247 27 30 162zの要素として30より大きいものの平均値を求める:[ ]内に「z(の要素)が30より大きい」、という条件を書き、関数 meanを適用すればよい> 平均 (z[z] > 30) [1] 40.55556要素を小さい順から並べて前から5番目までの要素を返す式:sort(z)でzの要素を小さい順から並べるベクトルを考えればいいと思います> 출구(z) [1:5] [1] 27 7 9 16奇数要素のみを返す式:奇数というのは2で割ったときの残りが1である。 それを条件に使用する。>z[(z% 2 == 1)] [1] 33 29 49 7 41 39 7 27 37[課題2-4の答え]関数ex2.4のカイン数をxに置き、『関数本体』がどうなるべきかを考えてみよう。ひとまず平均値mを求める式は関数meanを使ってm<-mean(x)と書く。 ここで各要素とmの差を二乗するベクトルは(x-m)**2と書くことができるので、この総和(sum)を求めればよい。 いわば以下のように書くことができる:ex2.4 <-function(x) { m <- mean(x) 리턴(sum(x-m)**2) }注意:関数を作ったことに満足せず、実際に様々な値で実験をしてみることhtp://lang.sist.chukyo-u.ac.jp/classes/R/Rintro-01.htmlR해설(1) R의 기초 R의 기초에 대해 배우다 이번 학습항목 R의 기본조작 R의 기본연산, 함수, 상수 대입 벡터 함수를 만드는 방법 R을 내 컴퓨터에 설치하기 위한 방법은 교과서 1장에 소개되어 있습니다.웹 검색하면 ‘R 간편 설치’ 같은 사이트도 많이 찾을 수 있을 거예요.컨, R 식 이 트 에 에 여 ) … download ) 하 오 우 택 대 , 의 각 도 우 os 의 lang.sist.chukyo-u.ac.jpR해설(1) R의 기초 R의 기초에 대해 배우다 이번 학습항목 R의 기본조작 R의 기본연산, 함수, 상수 대입 벡터 함수를 만드는 방법 R을 내 컴퓨터에 설치하기 위한 방법은 교과서 1장에 소개되어 있습니다.웹 검색하면 ‘R 간편 설치’ 같은 사이트도 많이 찾을 수 있을 거예요.요컨대, R 의 공식 사이트에서 Download and Install R 의 항에서 Download R for Windows (윈도우 OS 의 경우)나 Download R for Linux (Linux OS 의 경우) 를 선택하여 각각의 OS에 맞게 설치하십시오… lang.sist.chukyo-u.ac.jp코는 콧구멍이 나요.오늘은 금요일인데 시간이에요.원래, 나는 시간을 보냈다.우리 회사는 좋은 작업 레이블을 가지고 있습니다.1주일 정도 강의 번호 2주 동안 문을 열고 이웃들에게 그것을 받아들이지 않을 것입니다.


